Rajzolás pythonnal
##---- Pillangó egyszínű folyamatos vonallal
import numpy as np
import matplotlib.pyplot as plt
t=np.linspace(0,2*np.pi,300)
x = np.sin(t)*(np.exp(np.cos(t))-2*np.cos(4*t))
y = np.cos(t)*(np.exp(np.cos(t))-2*np.cos(4*t))
plt.plot(x,y,color='purple',linewidth=2)
plt.plot(-x,y,color='orange',linewidth=2)
plt.title("Pillangó egyszínű folyamatos vonallal",fontsize=14)
plt.axis("off")
plt.axis("equal")
plt.show()
## ---- Pillangó mintázat pontokkal és színátmenettel
import numpy as np
import matplotlib.pyplot as plt
t = np.linspace(0, 2 * np.pi, 300)
# Paraméterek a pillangó alakhoz
x = np.sin(t) * (np.exp(np.cos(t)) - 2 * np.cos(4 * t))
y = np.cos(t) * (np.exp(np.cos(t)) - 2 * np.cos(4 * t))
# Színátmenet létrehozása
colors = np.linspace(0, 1, len(t))
# Pillangó mintázat pontokkal és színátmenettel
plt.scatter(x, y, c=colors, cmap='plasma', s=10, edgecolors='none')
# Cím és formázás
plt.title("Színátmenetes pillangó mintázat", fontsize=14)
plt.axis("off")
plt.axis("equal")
plt.show()
## -------------- Pillangó mintázat kitöltése színátmenettel
import numpy as np
import matplotlib.pyplot as plt
t = np.linspace(0, 2 * np.pi, 300)
# Paraméterek a pillangó formához
x = np.sin(t) * (np.exp(np.cos(t)) - 2 * np.cos(4 * t))
y = np.cos(t) * (np.exp(np.cos(t)) - 2 * np.cos(4 * t))
# Színátmenet létrehozása a belső területhez
colors = np.linspace(0, 1, len(t))
# Pillangó mintázat kitöltése színátmenettel
plt.fill(x, y, color='green', alpha=0.2) # Alap szín, átlátszósággal
plt.fill(-x, y, color='orange', alpha=0.2) # A másik szárny kitöltése
# Cím és formázás
plt.title("Belső terület színezése", fontsize=14)
plt.axis("off")
plt.axis("equal")
plt.show()
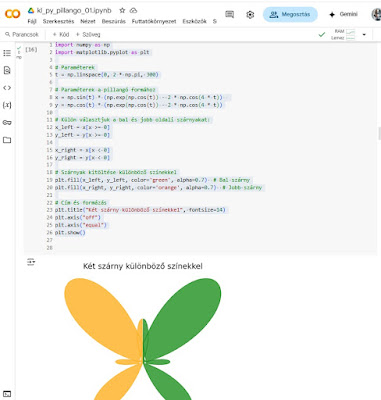
##------------ Szárnyak kitöltése különböző színekkel
import numpy as np
import matplotlib.pyplot as plt
# Paraméterek
t = np.linspace(0, 2 * np.pi, 300)
# Paraméterek a pillangó formához
x = np.sin(t) * (np.exp(np.cos(t)) - 2 * np.cos(4 * t))
y = np.cos(t) * (np.exp(np.cos(t)) - 2 * np.cos(4 * t))
# Külön választjuk a bal és jobb oldali szárnyakat:
x_left = x[x >= 0]
y_left = y[x >= 0]
x_right = x[x < 0]
y_right = y[x < 0]
# Szárnyak kitöltése különböző színekkel
plt.fill(x_left, y_left, color='green', alpha=0.7) # Bal szárny
plt.fill(x_right, y_right, color='orange', alpha=0.7) # Jobb szárny
# Cím és formázás
plt.title("Két szárny különböző színekkel", fontsize=14)
plt.axis("off")
plt.axis("equal")
plt.show()
## ----------------------- Gyönyörű Koch-hópehely létrehozása.
import numpy as np
import matplotlib.pyplot as plt
def koch_curve(p1, p2, depth):
"""Koch görbe rekurzív létrehozása két pont között."""
if depth == 0:
return [p1, p2]
p1 = np.array(p1)
p2 = np.array(p2)
v = (p2 - p1) / 3
p3 = p1 + v
p5 = p1 + 2 * v
angle = np.pi / 3
rotation_matrix = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]])
p4 = p3 + np.dot(rotation_matrix, v)
return (koch_curve(p1, p3, depth-1)[:-1] +
koch_curve(p3, p4, depth-1)[:-1] +
koch_curve(p4, p5, depth-1)[:-1] +
koch_curve(p5, p2, depth-1))
def koch_snowflake(order, scale=10):
"""Gyönyörű Koch-hópehely létrehozása."""
# Kezdő háromszög csúcsai
p1 = (0, 0)
p2 = (scale, 0)
p3 = (scale/2, np.sqrt(3) * scale / 2)
# Koch-fraktál alkalmazása a három oldalra
points = (koch_curve(p1, p2, order)[:-1] +
koch_curve(p2, p3, order)[:-1] +
koch_curve(p3, p1, order))
# További ágak generálása a fő hópehelyen belül
snowflake_x, snowflake_y = zip(*points)
plt.figure(figsize=(8, 8))
plt.plot(snowflake_x, snowflake_y, color='blue', linewidth=2)
# Színezés
plt.fill(snowflake_x, snowflake_y, color='deepskyblue', alpha=0.7)
# Háttér színezése
plt.gca().set_facecolor('midnightblue')
# Cím és formázás
plt.title("Még Szebb Hópehely Fraktál", fontsize=16, fontweight='bold', color='white')
plt.axis('equal')
plt.axis('off')
plt.show()
# Hópehely generálása magasabb részletességgel
koch_snowflake(order=5)
## -------------------- Sierpiński háromszög fraktál
import matplotlib.pyplot as plt
import numpy as np
# Sierpiński háromszög fraktál
def sierpinski_triangle(x1, y1, x2, y2, x3, y3, level):
if level == 0:
# Alap háromszög kirajzolása
plt.fill([x1, x2, x3], [y1, y2, y3], color='blue', edgecolor='black')
else:
# A három csúcs középpontjainak kiszámítása
xm1 = (x1 + x2) / 2
ym1 = (y1 + y2) / 2
xm2 = (x2 + x3) / 2
ym2 = (y2 + y3) / 2
xm3 = (x3 + x1) / 2
ym3 = (y3 + y1) / 2
# Rekurzív hívás a három kisebb háromszögre
sierpinski_triangle(x1, y1, xm1, ym1, xm3, ym3, level - 1)
sierpinski_triangle(xm1, ym1, x2, y2, xm2, ym2, level - 1)
sierpinski_triangle(xm3, ym3, xm2, ym2, x3, y3, level - 1)
# Paraméterek
level = 4 # Rekurzió szintje
# Háromszög csúcsai
x1, y1 = 0, 0
x2, y2 = 1, 0
x3, y3 = 0.5, np.sqrt(3) / 2
# Sierpiński háromszög fraktál generálása
plt.figure(figsize=(6, 6))
sierpinski_triangle(x1, y1, x2, y2, x3, y3, level)
plt.title("Sierpiński Háromszög Fraktál", fontsize=14)
plt.axis('equal')
plt.axis('off')
plt.show()
##----------
import numpy as np
import matplotlib.pyplot as plt
# Paraméterek
t = np.linspace(0, 2 * np.pi, 1000)
# Szív formájú egyenletek (simított változat)
x = 16 * np.sin(t)**3
y = 13 * np.cos(t) - 5 * np.cos(2*t) - 2 * np.cos(3*t) - np.cos(4*t)
# Ábrázolás
plt.figure(figsize=(6, 6))
plt.plot(x, y, color='darkred', linewidth=2) # Sötétpiros vonal
plt.fill(x, y, color='pink', alpha=0.7) # Rózsaszín kitöltés magasabb átlátszósággal
plt.title("Szép Szív Forma", fontsize=16, fontweight='bold', color='darkred')
plt.axis('equal')
plt.axis('off')
# Árnyékolás hozzáadása
plt.gca().set_facecolor('lightpink') # Háttér színezése világos rózsaszínre
plt.show()
##--------------------------- Rozetta
import numpy as np
import matplotlib.pyplot as plt
# Paraméterek
R = 10 # Nagy kör sugara
r = 3 # Kis kör sugara
d = 6 # Középponttól való eltérés (kitérés)
t = np.linspace(0, 20 * np.pi, 1000) # Paraméteres t időintervallum
# Rozetta egyenletek
x = (R - r) * np.cos(t) + d * np.cos((R - r) / r * t)
y = (R - r) * np.sin(t) - d * np.sin((R - r) / r * t)
# Ábrázolás
plt.figure(figsize=(6, 6))
plt.plot(x, y, color='purple', linewidth=2)
plt.title("Rozetta Minta", fontsize=14, fontweight='bold', color='purple')
plt.axis('equal')
plt.axis('off')
# Háttérszín beállítása
plt.gca().set_facecolor('lavender')
plt.show()
##-------------------------- Barnsley-páfrány
import matplotlib.pyplot as plt
import numpy as np
# Barnsley-páfrány generálás
def barnsley_fern(iterations):
# Kezdeti pont
x, y = 0, 0
# Üres listák a koordináták tárolására
x_vals = []
y_vals = []
for _ in range(iterations):
# Véletlenszerűen választott transformáció
r = np.random.rand()
if r < 0.01:
# A bal alsó kanyar
x, y = 0, 0.16 * y
elif r < 0.86:
# A bal alsó szárny
x, y = 0.85 * x + 0.04 * y, -0.04 * x + 0.85 * y + 1.6
elif r < 0.93:
# A jobb felső szárny
x, y = 0.2 * x - 0.26 * y, 0.23 * x + 0.22 * y + 1.6
else:
# A jobb alsó kanyar
x, y = -0.15 * x + 0.28 * y, 0.26 * x + 0.24 * y + 0.44
# Koordináták hozzáadása a listákhoz
x_vals.append(x)
y_vals.append(y)
return x_vals, y_vals
# Paraméterek
iterations = 100000 # Iterációk száma
# Barnsley-páfrány generálása
x_vals, y_vals = barnsley_fern(iterations)
# Ábrázolás
plt.figure(figsize=(6, 6))
plt.scatter(x_vals, y_vals, color='green', s=0.1) # Kicsi pontokkal
plt.title("Barnsley Páfrány Fraktál", fontsize=14)
plt.axis('equal')
plt.axis('off')
plt.show()

Megjegyzések
Megjegyzés küldése