MandelbrotFractal
A fraktálok végtelenül komplex geometriai alakzatok, amelyek határoló vonalai vagy felületei végtelenül „gyűröttek” vagy „érdesek”, illetve „szakadásosak” (szakkifejezéssel, nem differenciálhatóak)” Innen nyerték nevüket is a latin fractus melléknév, a frangere, „törni” ige származéka, ugyanis elsősorban töröttet, darabosat (vö. „mindenütt tüskésség” vagy „mindenütt szakadásosság”), másodsorban szabálytalant, kivételest jelent. Benoit B. Mandelbrot, a fogalom névadója ebből a latin szóból alkotta meg a fraktál kifejezést.
(Wikipedia)
A természet számos olyan objektummal rendelkezik, amelyek többszöri nagyítás után is részletesen struktúráltak, még egy erős mikroszkóp alatt is "gyűröttek" maradnak.
A tudósok csak az utóbbi évtizedekben ismerték föl, hogy ezekkel az alakzatokkal érdemes foglalkozni.
A fraktálgeometria a természet egyesülési, elágazási vagy törési folyamatainak mindegyikében megjelenő minták szimmetriájára mutat rá és rendkívül alkalmas azoknak a természeti jelenségeknek a modellezésére, amelyek több hosszúsági skálán is szabálytalanságot mutatnak.
A fraktálok két csoportra oszthatók: szabályos és véletlen fraktálokra .
A természetben előforduló fraktálok a második csoporthoz tartoznak, jellemző tulajdonságuk az önhasonlóság, vagyis az objektum egy része az egész objektumhoz – statisztikai értelemben – hasonló.
Bizonyos szempontból a folyamatok és a jelenségek invariánsak a skála-függő transzformációkra, mint például az egyszerű kicsinyítés vagy nagyítás.
Pythonban így tudunk ilyet generálni:
## import math from PIL import Image ## Size imgx = 800; imgy = 800 image = Image.new("RGB", (imgx, imgy)) pixels = image.load() ## generator parameters xa = -2.0; xb = 1.0 ya = -1.5; yb = 1.5 maxIt = 500 # of iterations number ## find max values for |x|, |y|, |z| maxAbsX = 0.0; maxAbsY = 0.0; maxAbsZ = 0.0 for ky in range(imgy): b = ky * (yb - ya) / (imgy - 1) + ya for kx in range(imgx): a = kx * (xb - xa) / (imgx - 1) + xa c = complex(a, b); z = c for i in range(maxIt): z = z * z + c if abs(z) > 2.0: break if abs(z.real) > maxAbsX: maxAbsX = abs(z.real) if abs(z.imag) > maxAbsY: maxAbsY = abs(z.imag) if abs(z) > maxAbsZ: maxAbsZ = abs(z) ## paint pictures for ky in range(imgy): b = ky * (yb - ya) / (imgy - 1) + ya for kx in range(imgx): a = kx * (xb - xa) / (imgx - 1) + xa c = complex(a, b); z = c for i in range(maxIt): z = z * z + c if abs(z) > 2.0: break v0 = int(255 * abs(z.real) / maxAbsX) v1 = int(255 * abs(z.imag) / maxAbsY) v2 = int(255 * abs(z) / maxAbsZ) v3 = int(255 * abs(math.atan2(z.imag, z.real)) / math.pi) v = v3 * 256 ** 3 + v2 * 256 ** 2 + v1 * 256 + v0 ## Colour generator colorRGB = int(16777215 * v / 256 ** 4) red = int(colorRGB / 65536) grn = int(colorRGB / 256) % 256 blu = colorRGB % 256 pixels[kx, ky] = (red, grn, blu) ## picture local save image.save("ColoursMandelbrotFractal.png", "PNG")
# Python code for Julia Fractal
from PIL import Image
import matplotlib.pyplot as plt
# setting the width, height and zoom of the image to be created
# w, h, zoom = 1920,1080,1
w, h, zoom = 800, 700, 1
# creating the new image in RGB mode
img = Image.new("RGB", (w, h), "red")
# Allocating the storage for the image and loading the pixel data.
pix = img.load()
# setting up the variables according to the equation to create the fractal
cX, cY = -0.7, 0.27015
moveX, moveY = 0.0, 0.0
maxIter = 255
for x in range(w):
for y in range(h):
zx = 1.5*(x - w/2)/(0.5*zoom*w) + moveX
zy = 1.0*(y - h/2)/(0.5*zoom*h) + moveY
i = maxIter
while zx*zx + zy*zy < 4 and i > 1:
tmp = zx*zx - zy*zy + cX
zy,zx = 2.0*zx*zy + cY, tmp
i -= 1
# convert byte to RGB (3 bytes), kinda // magic to get nice colors
pix[x,y] = (i << 21) + (i << 10) + i*8
# to display the created fractal
img.show()
plt.imshow(img, cmap='hot')
plt.axis("off")
plt.show()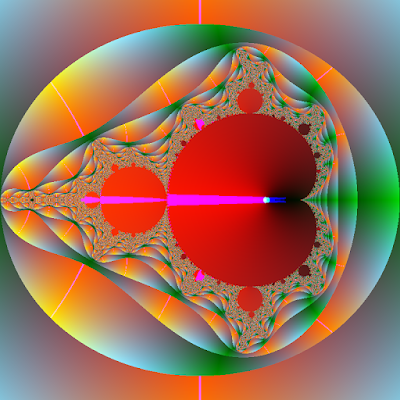







Megjegyzések
Megjegyzés küldése